Which Operation Can Be Used With the Augmented Matrix Below

The first equation should have a leading coefficient of 1. Add row 2 and column 3.

Solved On The Augmented Matrix Below Perform All Three Chegg Com

The first equation should have a leading coefficient of 1.

. Form the augmented matrix by the identity matrix. The row operations which correspond to multiplication by an invertible matrix on the left preserve the row space the linear span of the rows and the null space. True because elementary row operations are always applied to an augmented matrix after the solution has been found.

The augmented matrix below can be reduced to row-echelon form with a single row operation where we do not require leading entries to be 1 for REF. Answer to Solved 2. 1 3 1 0 1 1 R 1 3 R 2 R 1 1 0 4 0 1 1 1 3 1 0 1 1 R 1 3 R 2 R 1 1 0 4 0 1 1 We have the augmented matrix in the required form and so were done.

The solution to this system is x 4 x 4 and y 1 y 1. False because the elementary row operations augment the number of rows and columns of a matrix. Multiply each entry of a single row by a nonzero quantity.

There are three row operations that we can perform each of which will yield a row equivalent matrix. Which operation can be used with the augmented matrix below. Performing row operations on a matrix is the method we use for solving a system of equations.

Replace Row with X Row Row Carry out the indicated row operation then solve the resulting system by backward substitution. The goal is usually to get the left part of the matrix to look like the identity matrix. Multiply each entry of one row by some quantity and add these values to the entries in the same columns of a second row.

Interchange rows or multiply by a constant if necessary. Which operation can be used with the augmented matrix below. Can be represented by what is called an augmented matrix as seen below.

Row operations are calculations we can do using the rows of a matrix in order to solve a system of equations or later simply row reduce the matrix for other purposes. Use row operations to obtain zeros down the first column below the first entry of 1. 1 0 6 12 0 1 -2 0 0 0 0 0 a Use the reduced matrix to write down the parametric solution for the system as a point x y z.

Hence the result should be. Use row operations to obtain a 1 in row 2 column 2. Will transform an m n matrix into a different matrix of the same size.

The column operations preserve the column space the linear span of the columns and the null space of the transpose but they dont preserve the row space or the null space. R1 - 1 1 2 7. This means that if we are working with an augmented matrix the solution set to the underlying system of.

2 0 0 0 1 0. The matrix operation denoted as R1R2 means that the First and Second rows of the Augmented matrix are interchanged in the resulting matrix. Here is the operation for this final step.

Write the system as an augmented matrix. From the final augmented matrix we found in Step 5 we get the solution to the system is. True because the elementary row operations replace a system with an equivalent system.

Given an augmented matrix perform row operations to achieve row-echelon form. The augmented matrix below represents a system of linear equations associated with a real world prob- lem. Up to 10 cash back There are 3 basic operations used on the rows of a matrix when you are using the matrix to solve a system of linear equations.

Row 1 R 1 0 8 16 0 Row 2 R 2 1 0 -3 1 Row 3 R 3 -4 14 2 6 x y z constant Coefficients of the three unknown variables x y and z and the constant terms are placed in. 1 7 11 0 1 1 R 1 7 R 2 R 1 1 0 4 0 1 1 1 7 11 0 1 1 R 1 7 R 2 R 1 1 0 4 0 1 1 Show Step 6. Given an augmented matrix perform row operations to achieve row-echelon form.

All the augmented matrices obtained on the right correspond to the system of equations on the left and we can therefore solve any system of linear equations using augmented matrices. 4 11 1 0 0 9 6 -7 3 6 13 8 Complete the description of this row operation. Swap the location of two rows.

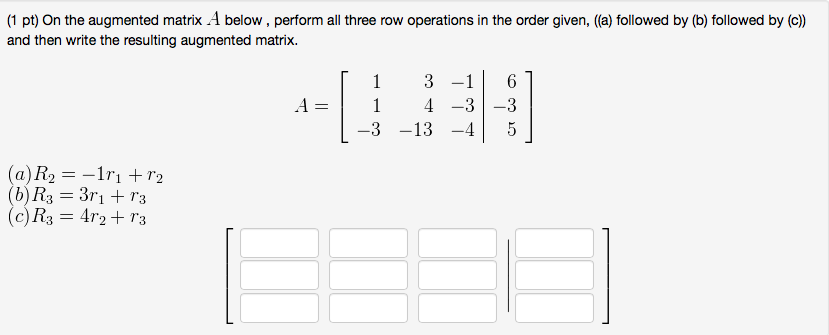
R2 - 3 2 1 4. We are interested in the first and second rows of the matrix R1 and R2 respectively as the third row R3 will remain unchanged. On the augmented matrix A below perform all three row operations in the order given a followed by b followed by c and then write the resulting augmented matrix.

O multiply row 3 by 0. 0n the augmented matrix A below perform all three row operations in the order given. Interchange rows or multiply by a constant if necessary.

15 3 2 1 1 5 8-2 -1 3 1 switch column 1 and column 2. Multiply row 3 by 0. Multiply row 2 by-1 and add it to row 3.

X 4 y 1 x 4 y 1. The three operations are. Using row operations on an augmented matrix to achieve row-echelon form.

Add row 2 and column 3. Rows operations are used to rewrite augmented matrices in reduced row echelon form which is itself used to solve systems of equations find inverse of matrices check linearity of vectors in linear. Consider the augmented matrix below.

Multiplying a Row by a Number. Use row operations to obtain a 1 in row 2 column 2. The augmented matrix has already been completely row reduced.

Now that we can write systems of equations in augmented matrix form we will examine the various row operations that can be performed on a matrix such as addition multiplication by a constant and interchanging rows. Use row operations to obtain a 1 in row 2 column 2. To do that we can use the following elementary row operation.

The augmented matrix below represents a system of. Use row operations to obtain zeros down the first column below the first entry of 1. Interchange rows or multiply by a constant if necessary.

Switch column 1 and column 2. Use row operations to obtain zeros down the first column below the first entry of 1. The first equation should have a leading coefficient of 1.

A matrix is in reduced row echelon form RREF if. There are 3 basic operations used on the rows of a matrix when you are using the matrix to solve a system of linear equations.

Solved On The Augmented Matrix Below Perform All Three Chegg Com

The Augmented Matrix Below Represents A System Of Equations Brainly Com

Solved Kamal Wrote The Augmented Matrix Below To Represent A Chegg Com